焼結機構の結果と考察 ｜セラミックス技術コラム

A. ガラス
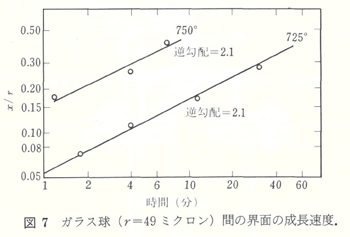
　図7に、log⁡(x/r)とlog t のプロットを示すように装置と本方法の妥当性を試すため、ガラスの焼結の予備試験が行われた。約2の逆数勾配は前報の結果と一致しており、粘性流動が式（1）で示される起こることを示している。これらのデータから計算された粘性係数（γ=313 dyne cm^-1の場合）は、725 ℃で7.2×10⁸ ポワズ、750 ℃で8.8×10⁷ ポワズであり、予想された結果とよく一致する。

B. 塩化ナトリウム
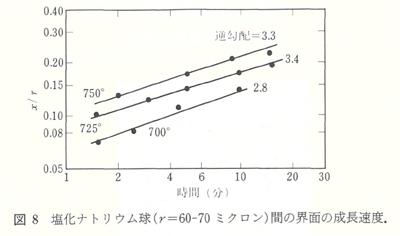
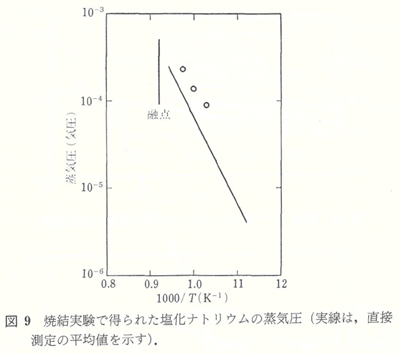
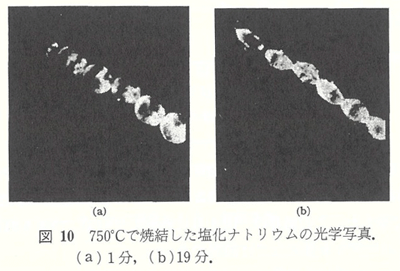
　塩化ナトリウムの61.5-70ミクロン球径試料の焼結速度の測定は、図8に示すように700-750℃で行われた。得られた逆数勾配2.8-3.4は蒸発凝縮機構に対応している。式（6）から計算される蒸気圧は、直接蒸気圧測定¹⁵⁾の平均値と比較して図9に示されている。計算の絶対値は、2倍ほど大きいが、温度の依存性は良く一致している。これは近似解析から予想されるよりも、良い一致である。塩化ナトリウム球の中心間の距離は、実験的に測定しうるほど、変わらなかった。しかし、個々の球は、図10に示すように、だ円形になった。
　これらすべての観察結果は、蒸発凝縮過程で焼結することを示している。そして無収縮の観察結果は、このプロセスが成形体の緻密化に寄与しないことを実験的に示唆している。この観察の結果をさらにチェックするため、種々の粒度の塩化ナトリウムの成形体を、750℃で焼結したが、無収縮であった。しかし、強度は著しく増加した。この結果は、電子顕微鏡観察¹⁶⁾の結果と一致し、前報の焼結挙動とも一致した^17,18）。

C. 銅
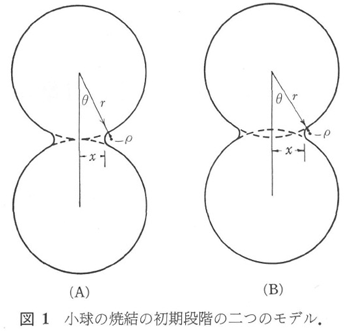
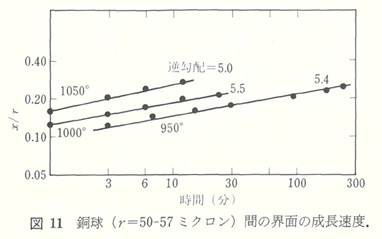
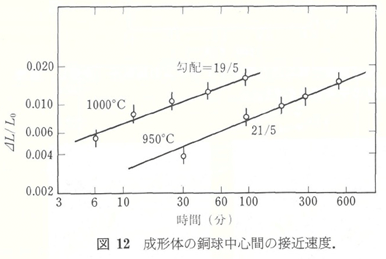
　直径約100 ミクロンの銅球の焼結挙動の測定を950-1050℃で行い、図11に示すような結果を得た。観察された逆数勾配の5.0-5.5は、拡散プロセスに対応している。球の中心間の距離の減少は体積拡散が起こっていることを示す結果と思われる。ここで考えられた焼結モデル（図1Aと図1B）は、球の中心の接近する速度を測定することによって調べることができる。銅球のデータを、図12に示した。この結果は、図1Bに合致している。つまり時間の依存性も収縮の大きさも、図1Aのモデルを基にしては説明できない。
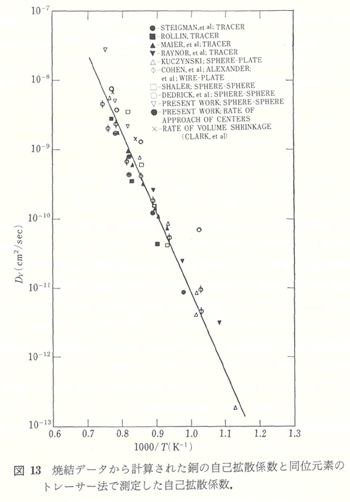
　式（16）から計算された自己拡散係数は、収縮の速度に対応している。これを焼結から計算した結果^{(注),1,4,6,8)}（γ=1670 dyne cm^-1を用いた）と同位元素の測定結果^19~22)と共に、図13に示した。同位元素を用いた測定の拡散係数の平均値は、D=2.7exp⁡(-53000/RT)であり、焼結測定も同一の結果となった。この絶対値の一致、および多くの実験者の焼結データから計算された拡散係数と直接同位元素で測定した値の一致は、体積拡散機構により焼結することを示している。そして、粒径の異なる同様の焼結は、体積拡散の場合（∆t₁=λ³ ∆t₂）のHerringのスケール測に一致する。
　拡散係数は、また球の中心の接近する速度（図12）と式（26）から計算することができる。計算の結果は、図13に示されている。それはまた球のネック部の成長速度から計算される結果と良く一致する。
　球形粒子の成形体の体積の収縮速度は、本稿のモデルの場合、式（27）で与えられる。すなわち、
　

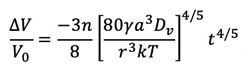
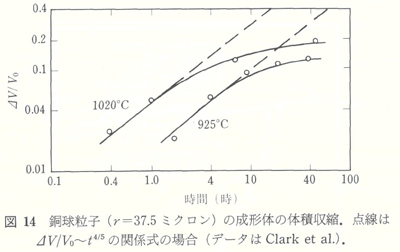
銅球粒子（γ=37.5 ミクロン）の成形体の体積収縮の場合に、Clark, Cannon, White23)によって報告されたデータが図14に示されている。観察された初期焼結の時間依存性は、式（27）によって良く表された。式（27）によって計算された拡散係数は、図13に示されており、それら他のデータと良く一致する。自己拡散係数の絶対値、ネック成長の速度、中心間の近接する速度および成形体の体積収縮の速度などから計算される自己拡散係数の温度依存性の一致は、すべて利用しうる初期焼結のデータが図1Bに示したモデルの自己拡散に律速されるプロセスに一致することを示している。このモデルは、体積拡散の物質の源が、前述のように、球の表面ではないことを必要としている。格子空孔は、転位ないしは粒子間の粒界で消滅すると思われる。カーケンダール効果の存在は、格子空孔を転位で消滅させることを可能にする。しかしながら、高温では小さな応力でも銅のワイヤーが流動することに粒界が寄与すること²⁴⁾、気孔の収縮が粒界の存在によって著しく加速されること²⁵⁾などは、格子空孔が粒界で主に消滅することを、より確かなものにしている。拡散における複雑な境界条件は、焼結データから計算される定量的な拡散係数に信頼を置けなくしている。しかしながら、観察されたおおよその値と、温度依存性（活性化エネルギー）は信頼しうるのである。

（注）次の場合に式（16）の等価な式から再計算された。
板上の球の場合
　

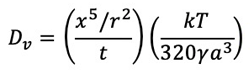
板上のワイヤーの場合
　

これらの値は、もとの式で計算した値と違っている。
　
　

D. Al₂O₃sup>とZrO₂
　界面の成長速度の測定は、温度範囲1500から2200℃、50-150ミクロンの球で行った。球体間の結合は、1300℃で起こることが観察された。溶融アルミナと溶融安定化ジルコニアについて行った測定は、x/r=0.2 まで粒界面の急速な増加を示し、それからゆっくりと増加した。しかし、結果は非常にバラついた。同様に焼結した一群の球は、図15に示すように、大変違った挙動を示している。高純度のアルミナとジルコニアの試料は、短時間にx/r～0.2 になり、100分までの値はアルミナの場合2020℃まで、ジルコニアの場合2200℃まで、実験の誤差範囲でx/r の値は変わらないままであった。これらの測定に加えて、密度の低い成形体と緻密な成形体（41,000 psi）がつくられ、同時に1800 ℃に加熱された。前者は測定しうるほどの密度の変化が起こらないのに対して、後者は、22.7 ％の線収縮率を示した。これらの結果は、ここで観察された粒径（50-100 ミクロン粒径）では表面エネルギーが識別可能なほどに焼結するには不十分であることを示している。しかし、十分な歪エネルギー（粒子の破壊は観察されないが、歪エネルギーは接触点で起こるかもしれない）を導入する成形は、焼結速度を促進するかもしれない。

結論
　ガラス球の焼結は、粘性流動プロセスに一致することが観察された。塩化ナトリウム球の焼結は、蒸発凝縮によって起こる。蒸気圧の計算値とその温度依存性は、直接測定のデータと良く一致する。このプロセスでは、収縮と緻密化は起こらない。
　銅球の焼結データは、粒界あるいは多分転位が格子空孔の消滅場所となる体積拡散のモデルに良く一致する。このモデルは、界面の成長、線収縮、粒径の影響の時間と温度の依存性に良く一致する。
　アルミナとジルコニアの球状粒子（50-100 ミクロン粒径）の焼結データは、融点の近傍の温度でも、ほとんど焼結しないことを示している。適当量の不純物が焼結において著しい影響のあることが観察された。

参考文献
1) Kuczynski, G. C. : Trans. Am. Inst. Mining Met.Engrs., 185, 169 (1949).
2) Herring, C. : J. Appl. Phys., 21, 301 (1950).
3) Kuczynski, G. C. : J. Appl. Phys., 21, 632 (1950).
4) Cohen, G. and Kuczynski, G. C.: J. Appl. Phys., 21, 1339 (1950).
5) Dedrick, J. H. and Gerds, A : J. Appl. Phys., 20, 1042 (1949).
6) Shaler, A. J.: Trans. Am. Inst. Mining Met.Engrs., 185, 796 (1949).
7) Kuczynski, G. C.: J. Appl. Phys., 20, 1160 (1949).
8) Alexander, Kuczynski and Dawson : Relations between Diffusion and Viscous Flow in Metals, p. 202, The Physics of Powder Metallurgy, Kingston, W.E., Editor. (McGraw-Hill Book Company, Inc., New York, 1951).
9) Frenkel, J. : J. Phys.(U.S.S.R.), 9, (5), 385 (1945).
10) Cabrera, N. : Trans. Am. Inst. Mining Met. Engrs., 188, 667 (1950).
11) Schmed, P. : Trans. Am. Inst. Mining Met. Engrs., 191, 245 (1951).
12) Wedmore, E. B. : J. Inst. Elec. Engrs. (London), 61, App. IV (1923), 68, App. I (1930).
13) Pines, B. Y. : J. Tech. Phys. (U.S.S.R), 16, 737 (1946).
14) Ivensen, V.A. : J. Tech. Phys. (U.S.S.R), 17, 1301 (1947).
15) Kubashewski, O. and Evans, E. L. : Metallurgical Thermo-chemistry (Butterworth-Springer Ltd., London, 1951).
16) Endel, E. and Ardenne, M. V. : Z.Kolloid., 104, 223 (1943).
17) Mueller, H.V. : Z. Physik., 96, 279, 307, 321 (1935).
18) Smekal, A.G.: Mechanism of Crystal Growth, in The Physics of Powder Metallurgy, Kingston, W. A., Editor. (McGraw-Hill Book Company, Inc., New York, 1951), Chap. 2.
19) Raynor, Thomassen and Rouse : Trans. Am. Inst. Mining Met. Engrs., 30, 313 (1942).
20) Maier, M.S. and Nelson, H. R. : Trans. Am. Inst. Mining Met. Engrs., 147, 39 (1942).
21) Rollin, D.V. : Phys. Rev., 55, 231 (1939).
22) Steigman, Shackley and Nix : Phys. Rev., 56, 13 (1939).
23) Clark, Cannon and White : Trans. Brit. Ceram. Soc., 52, 1 (1953).
24) Greenough, A. P : R. A. E.Tech. Note No. MET 151 (October,1951).
25) Alexander, B. H. and Balluffi, R. : J. Merals, 188, 1219 (1950).

Journal of Applied Physics, vol.26, No. 10, pp. 1205-1212 (1955)

宗宮 重行・守吉 佑介 共編　「焼結－ケーススタディ」