D.　焼結機構の実験的決定 ｜セラミックス技術コラム

　焼結機構の正確な決定は、複合機構の影響によって複雑である。例えば拡散の場合には、表面拡散と体積拡散の時間的依存性の類似によって複雑になる。加えて、クリープや塑性流動が重要になるような場合に、実験的な応力－歪関係が、焼結速度の関数に入るかもしれないから、どんな単純な解析によっても論じえないような焼結速度になるであろう。計算の速度の絶対値（すなわち、粘性係数、蒸気圧、拡散係数と定量的に一致すること）、Herringのスケール則、および正しい温度依存性を示すデータのみが、信頼して受け入れられる。
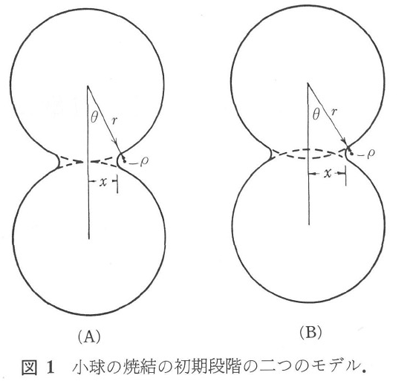
　表面拡散と蒸発凝縮を粘性流動、クリープ、体積拡散から分けるもう一つの方法は、図1における粒子の中心間の距離の減少を観察することによってなされる。もしも、蒸発－凝縮と表面拡散が起こるならば、中心間の距離は変わらない（したがって、成形体の収縮はない）^6,13,14)。
　球の近接する速度を考えるならば、ネック部分に満たされてゆく体積を計算する必要がある。そして、粘性流動や体積拡散の場合には、等価な量の体積減少が保たれることを必要とする（図1Aに対応）。この場合、V=πx⁴/2rで粘性流動の場合、式（1）から、
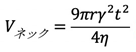 　(17)
              
その結果、一つの接触点当たりの球の体積減少は次式で与えられる。
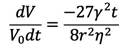　(18)

もしも接触の数がnであると、球の成形体の場合も次式のようになる。
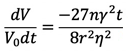　(19)

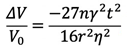　(20)

同様に、体積拡散の場合、図1（A）のケースでは、式（14）から
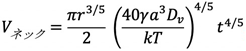　(21)

その結果、n個の接触点をもつ球の体積減少は、次式で与えられる。
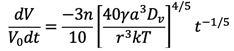　(22)

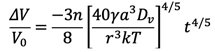　(23)

これらの式は、約2 %の体積収縮まで、かなり正確に成り立つことが期待されるが、6 %以上の収縮では完全に成り立たなくなる。拡散の場合のように、小さな収縮率（3ΔL/L₀≅ΔV/V₀）では、式（23）と等価になって、
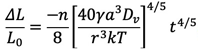　(24)

図1（B）を仮定した場合、接近の速度は、かなり大きく、次式で与えられる。
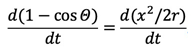　(25)

この関係式を式（16）と結びつけて、次のようになる。
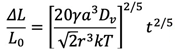　(26)

体積収縮は式（16）から次のように与えられる。
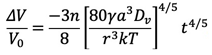　(27)

 

宗宮 重行・守吉 佑介 共編　「焼結－ケーススタディ」