粘性流動、蒸発凝縮、自己拡散による焼結 ｜セラミックス技術コラム

　焼結における物質移動の機構は、粒子の接合面の成長速度および粒子間の収縮速度を直接観察することによって説明できる。ガラス、塩化ナトリウム、銅の測定結果は、これらの物質移動がそれぞれ粘性流動、蒸発凝縮および自己拡散によって律則されることを示している。粘性係数、蒸気圧、拡散係数が、それぞれの機構の場合に測定された。しかし、データより計算した拡散係数の解釈は今後に残された。粒界や転位で格子空孔が消滅するというモデルは、初期焼結における銅の焼結挙動を良く表し、実験データと良く一致した。酸化物の焼結では、不純物や雰囲気の重要性が示唆された。しかしながら、本実験データから焼結機構は決められなかった。

緒言
　接触した粒子が結合して一つの固体に成長する焼結プロセスは、大変複雑である。時間と共に変化する密度、電気伝導度およびその他の焼結体の性質を明確に解釈するのは難しい。初期焼結だけを取り出すには小球を接触させて、接触面の増加速度を観察する手法が用いられる。この速度は物質移動の機構に依存する¹⁾。同様に、この場合の焼結速度における粒径の影響は、物質移動の機構に依存する^2）。これまでに接触面の増加速度の測定法が種々報告されている^1,3~8)。しかし、どの論文にも、厳密な解析に必要なデータとその方法の妥当性は述べられていない。本論文では、ガラス、塩化ナトリウム、銅などの焼結データを他のデータと比較しつつ論述する。

焼結速度の計算およびモデルからの焼結機構の決定
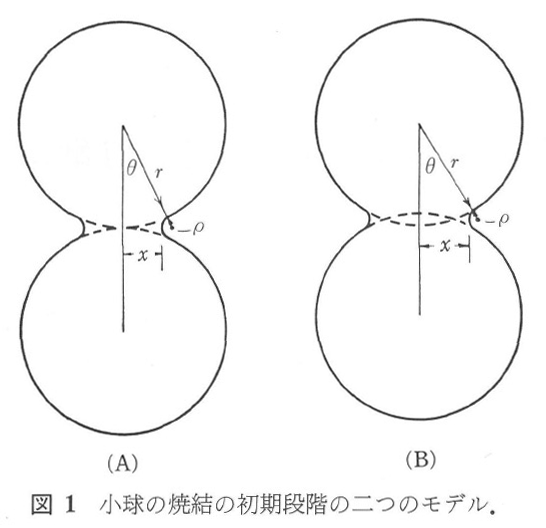
　粘性流動、塑性流動、蒸発凝縮、表面拡散、体積拡散など種々の物質移動が焼結過程で起こる。図1に示すように、二つの等大球粒子の焼結について、ここでは、粘性流動、蒸発凝固および拡散について考えてゆくことにしよう。焼結は、球体間に物質が満たされてゆくプロセス（図1A）、または球体の中心が接近するプロセス（図1B）によって進むと考えることができる。図1Aの場合に、球の半径rが焼結過程で変わらないとし、成長したネックの半径をxとすると、x / r <0.3の場合に、ネック表面の半径は、x² / 2 rと近似できる。二つの粒子の間に満たされた物質の体積は、πx⁴ / 2 r、ネックの面積は、π²x³ / 2 rと近似的に表せる。図1Bの場合には、ネック表面の半径は近似的にx² / 4 rであるから、ネックの体積はπx⁴ / 2 rで、ネックの面積はπ²x³ / 2 rで与えられる。物質移動の速度と体積変化の速度を数式化することによって、粒子間の接触界面成長の速度を推定することができる。


A. 粘性流動
　粘性流動の式は、Frenkel⁹⁾によって考えられた。ネックの成長と時間の関係は次のように与えられる。

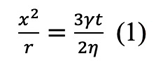
ここで、γは表面エネルギー、ηは粘性係数、tは焼結時間である。x² / rとtをプロットすると、勾配（3γ / 2η）の直線が得られる。

B. 蒸発凝縮
　図1に示すように、負の小さな曲面上の蒸気圧（P）は、表面エネルギーのいわゆる、ケルビンの式によって減少する。

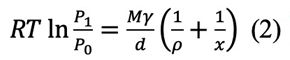
ここでP0は平面での平衡蒸気圧、Mは分子量、dは密度である。x>>ρであり、P0－P1＝ΔPは小さいから、ln P1 / P0＝ΔP / P0で、次のように書ける。

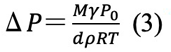
物質移動の速度にラングミュアーの式を近似すると、

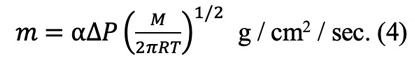
そこで、凝縮の速度が体積の増加に等しくなる。そして蒸発係数を1とすると、

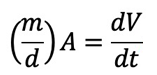
そして

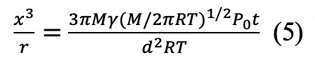
x³ / r とtをプロットすると、直線が得られ、勾配から蒸気圧が決められる。

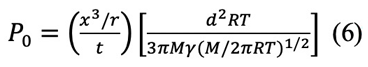
C. 拡散
　拡散による焼結速度の計算は、かなり不明の点があり複雑である。いずれにしても、ネックの曲面での自由エネルギーは、平らな面のそれより低いので、ρで格子空孔濃度が高く、そこへ向って拡散の流れが起こる。
　Cabrera¹⁰⁾、Schmed¹¹⁾ 、Kuczynski¹⁾は、それぞれ多少異なった表面拡散の式を考察している。粒径の異なる試料の場合、Herring²⁾によって示されたように、もしもr1=λr2であれば、形状変化に対応する時間の変化はΔt1=λ⁴Δt2で与えられる。
　ネック中への物質機構は、平らな表面から自由エネルギーの低いネックの部部への体積拡散で進行する。平面下の格子空孔より過剰な格子空孔濃度ΔNは次式で与えられる。

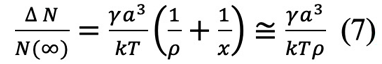
ここで、aは原子の半径、kはボルツマン定数である。格子空孔が、半径ρのネックの表面から半径rの円筒へ、格子空孔の濃度差ΔN、格子空孔の拡散係数D’で拡散すると、単位時間・単位長さ当たりの拡散する格子空孔の数は、

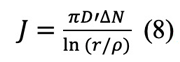
ここで、図1(A)により、ρ＝x² / 2r、V＝πx⁴ / 2 r、dV/dt=2πxa³J、Dv=a³D’N(∞)である。Dvは自己拡散係数である。

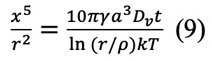
測定範囲ln r / ρ～4では、

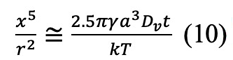
x⁵ / r³とtをプロットすると、直線が得られ、勾配からDvが得られる。

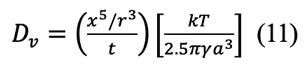
式(9)において、Kuczynski¹⁾はr / ρ≅2を用いているので、その結果、彼の解析では次式のようになる。

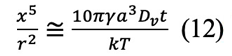
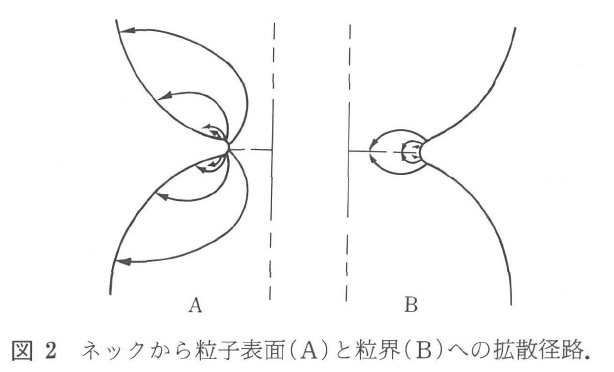
他方の拡散経路による解析は、格子空孔の濃度がネックを源とし、大球の表面で消滅して一定濃度に保たれると仮定する。この条件で式を解くのは難しい。しかしWedmore¹²⁾の図解によると、格子点の空孔がネック部分から単位時間単位長さ当たり図2(A)に示すような経路で拡散する。その結果、次式のようになる。

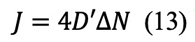
これを用いると、次式が得られる。

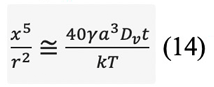
　もし、図1(B)に対応するモデルが仮定されると、明らかに、表面はネックから拡散する格子空孔の消滅場所としては働かない。その代わりに、粒子間の粒界が、図2(B)に示すような経路で格子空孔の消滅場所となる。格子空孔がネックから離れて、転位で消滅することもあり得る。粒界が消滅場所として働くと式(13)が良く適用できる。この場合、図1(B)によりρ＝x² / 4r、V＝πx⁴ / 2 r、そしてdV / dt=2πxa³Jであるから、その結果次のようになる。


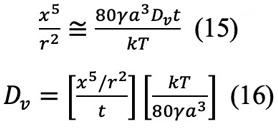
もしも粒径の異なる試料が観察されるならば、Herring²⁾によって示されているように、r1=λr2となるので、体積拡散による形状変化の相対的な時間はΔt1=λ³Δt2で与えられる。

宗宮 重行・守吉 佑介 共編　「焼結－ケーススタディ」